HELLO DOSTO !!
Today we will learn about a number system that computers can understand......
OBJECTIVES:-
♦ Digital Computers and Digital Systems
♦ Types of Number System
♦ Number-base Conversions
Decimal to other
other to Decimal

✪Digital Computers and Digital Systems
There are two types of signals:-
analog signal
Digital signal
✬Analog system
The signal may vary continuously over a specified region.

✬Digital system
The physical quantities or signals can assume only discrete values.
Greater accuracy

\=> Binary values
Digits 0 and 1
Words (symbols) False (F) and True (T)
Words (symbols) Low (L) and High (H)
And words On and Off
Block Diagram of Digital Computer

✬ Types of Number System
Decimal Number
Binary Number
Octal Number
Hexadecimal Number
Decimal Number: The system of numbers which has a base or radix is 10.....
ex. (512.74)10
Binary Number: The system of numbers which has a base or radix is 2.....
ex. (101.01)2
Octal Number: The system of numbers which has a base or radix is 8.....
ex. (512.74)8
Hexadecimal Number: The system of numbers which has a base or radix is 16.....
ex. (165.7A)16
✪ Number-base Conversions:-
Decimal to other:
Decimal to Binary:
Let us understand with an Example...
Q. (13.56)10
Quotient Remainder | Value after Point:-
13/2 = 6 1 | 0.56*2 = 1.12 1
6/ 2 = 3 0 | 0.12*2 = 0.24 0
3/2= 1 1 | 0.24*2 = 0.48 0
1/2= 0 1 | Take two or Three values
ANSWER: (13.56)10=(1101.100)2

✪ Decimal to octal
1. Convert (127)10 to Octal.
Solution: Divide 127 by 8
127 ÷ 8= 15(Quotient) and (7)Remainder
Divide 15 by 8 again.
15 ÷ 8 = 1(Quotient) and (7) Remainder
Divide 1 by 8, and we get;
1 ÷ 8 = 0(Quotient) and (1) Remainder
Hence, (127)10 = (177)8
✪ Decimal to Hexadecimal
Convert (960)10 into hexadecimal.
To convert decimal to hex, i.e. 960 base 10 to a hexadecimal number, follow the steps given below:
Step 1: First, divide 960 by 16.
960 ÷ 16 = 60 and remainder = 0
Step 2: Again, divide the quotient 60 by 16.
60 ÷ 16 = 3 and the remainder is 12.
Step 3: Again dividing 3 by 16, will leave quotient=0 and remainder = 3.
Step 4: Now taking the remainder in reverse order and substituting the equivalent hexadecimal value for them, we get,
3→3, 12→C and 0→0
Therefore, (960)10 = (3C0)16
Other to Decimal:-
Let us take an example
to understand how we convert
Binary to Decimal :
Q. (1011)2 -> ()10

Answer: (1011)2 -> (11)10
Binary to Octal :
Q. (101010011.110100)2 -> ()8

HINT:- _ _ _
4 2 1
ANSWER: (101010011.110100)2=(523.64)8
Binary to Hexadecimal :
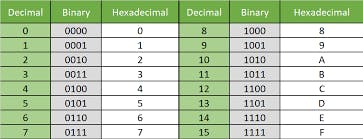
Table of number system represent in discreate system
Q. (11111011101110010)2 -> ()16
ANSWER: (11111011101110010)2 -> (1f8772)16
